Dnes se podíváme na problematiku simulace obyčejné diferenciální rovnice ODE v pythonu. Budeme využívat modul scipy, který obsahuje mnoho algortimů pro numerickou matematiku. Pro řešení dynamického systémů (ten je popsán diferenciálními rovnicemi) použijeme numerickou metodu. Rozdíl mezi numerickým a analytickém řešením je ten, že analytické řešení je zcela přesné, ale lze takto vyřešit jen omezenou sadu úloh. Naopak numerika je velmi používaná v inženýrské praxi.
Jak vypadá taková ODE?
\large\frac{dx}{dt}= ax Tak například výše máme ODE prvního řádu. Na levé straně máme derivaci x podle času. Pro tuto jednoduchou ODE je známé analytické řešení. Řešením ODE je funkce:
\large x(t)= e^{at}x(0)Take se můžeme setkat s termínem „řešení počátečního problému“. Můsíme tedy znát počáteční podmínku x(0).
My budeme řešit rovnice numerickou metodou. K tomu využijeme modul scipy a funkci solve_ipv. V prvé řadě musíme nadefinovat funkci, kterou bude numerická metoda volat a získávat tak řešení v každém výpačetním kroku. Dále interval na jakém budeme řešení chtít např. čas simulace. Bude potřeba zadata počáteční podmínky. Funkce solve_ipv také nabízí několik numerických metod. Pro začátek je nejvhodnější volit RK45. Jedná se o metodu s adaptivním krokem simulace. Velikost výpočetního kroku upravuje dle odhadu chyby řešení. Konkrétně se jedná o motedu z rodiny Runge–Kutta–Fehlberg, což je velmi dobrá explicitní metoda 4-5 řádu. Pro některé typy úloh však vhodná není. jedná se zejména o tzv. stiff problémy.
Vyřešíme jednoduchou ODE1 (prvního řádu)
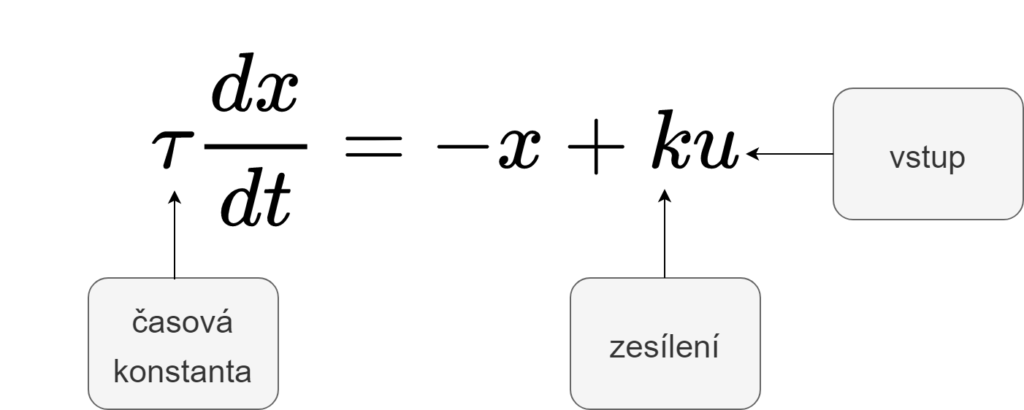
τ = 0.1
k = 10
u <0-0.1> = 0 ; <0.1-1> = 1
Vstupem tedy bude jednotkový skok v čase 0,1 s.
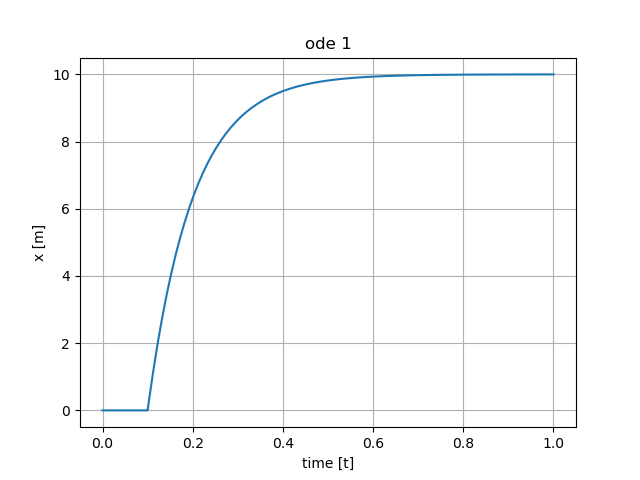
Příklad řešení vykreslen v matplotlib:
Dále vyřešíme rovnici, která je asi nejpoužívanější ve školním prostředí. Jedná se o hmotu s pružinou a tlumičem. Tento systém má i poměrně dobré praktické využití např. nejednodušší model zavěšení náprav automobilu.
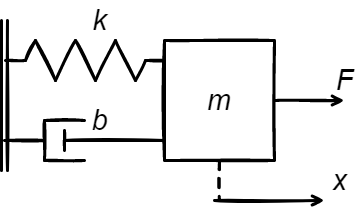
\large \ddot{x}m+\dot{x}b+ kx = F(t) Setrvačná, tlumící a potencionální (síla pružiny) je v tomto případě rovna budící síle. Tentokrát jsme použili tzv. Newtonův zápis. Jedna tečka nad x znaméná první derivaci podle času atd.
Při prvním pohledu zjistíme, že se jedná o ODE druhého řádu, což je typické pro mechanické systémy. Numerické řešiče řeší soustavy ODE prvního řádu a je tedy nutné naši rovnici upravit. Tato úprava je možná vždy a tedy rovnice vyšších řádů můžeme převést na soustavu rovnic řádu prvního.
Upravená ovnice vhodná pro simulaci bude vypadat takto:
\large \dot{x}=v \\ \dot{v} = \frac{1}{m}(F(t) - vb - xk)Takto upravená rovnice je už vhodná k simulaci. Jedná se o soustavu ODE, kde máme první derivace izolované na jední straně rovnic.
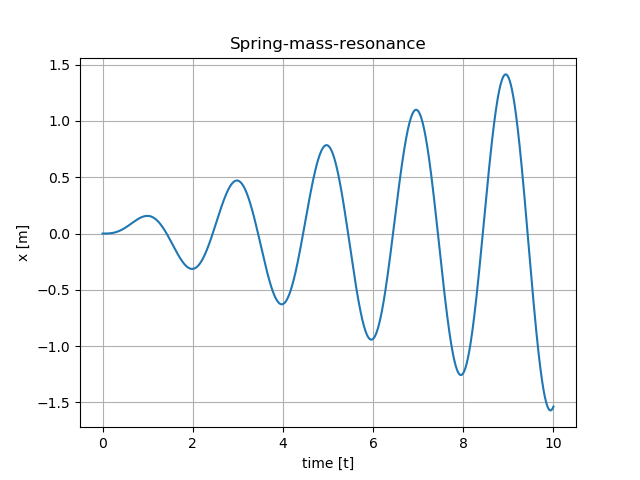
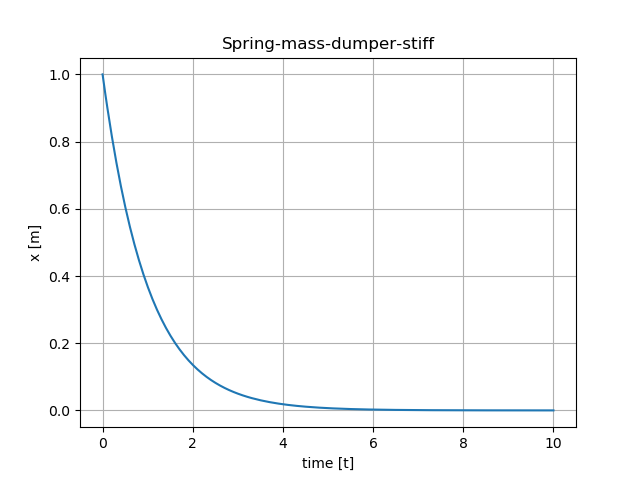
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 | import numpy as np from scipy import integrate import matplotlib.pyplot as plt def ode1(t, x): tau = 0.1 k = 10 if t < 0.1: u = 0 else: u = 1 dx = (-x + k * u) / tau return dx def ode2(t, x): F = 100 k = 10 b = 3 m = 1 dx1 = x[1] dx2 = (F - k*x[0] - b*x[1])/m dx = [dx1, dx2] return dx def ode3(t, x): F = 1 k = 10 b = 0 m = 1 omg = np.sqrt(k/m) dx1 = x[1] dx2 = (F*np.sin(omg*t) - k*x[0] - b*x[1])/m dx = [dx1, dx2] return dx def ode4(t, x): k = 1000 b = 1001 m = 1 dx1 = x[1] dx2 = (- k*x[0] - b*x[1])/m dx = [dx1, dx2] return dx def ode_sim(): xt2 = integrate.solve_ivp(fun=ode2, t_span=[0.0, 10.0], y0=[0.0, 0.0], max_step=0.01, method="RK45") xt1 = integrate.solve_ivp(fun=ode1, t_span=[0.0, 1.0], y0=[0.0, 0.0], max_step=0.01, method="RK45") xt3 = integrate.solve_ivp(fun=ode3, t_span=[0.0, 10.0], y0=[0.0, 0.0], max_step=0.01, method="RK45") xt4 = integrate.solve_ivp(fun=ode4, t_span=[0.0, 10.0], y0=[1.0, 0.0], max_step=0.1, method="BDF") plt.figure(1) plt.plot(xt2.t, xt2.y[0]) plt.title("Spring-mass-dumper") plt.xlabel("time [t]") plt.ylabel("x [m]") plt.grid() plt.figure(2) plt.plot(xt1.t, xt1.y[0]) plt.title("ode 1") plt.xlabel("time [t]") plt.ylabel("x [m]") plt.grid() plt.figure(3) plt.plot(xt3.t, xt3.y[0]) plt.title("Spring-mass-resonance") plt.xlabel("time [t]") plt.ylabel("x [m]") plt.grid() plt.figure(4) plt.plot(xt4.t, xt4.y[0]) plt.title("Spring-mass-dumper-stiff") plt.xlabel("time [t]") plt.ylabel("x [m]") plt.grid() plt.show() print(len(xt4.t)) if __name__ == '__main__': ode_sim() |